SVM(支撑向量机)是一种强壮的机器学习算法,广泛运用于分类和回归问题。以下是SVM的一些基本概念和原理:
1. 基本思想:SVM的方针是在特征空间中找到一个超平面,这个超平面能够将不同类其他数据点尽可能分隔。这个超平面称为“最优超平面”,它应该坐落两类数据点之间,而且距离两类数据点的距离最大化。
2. 线性SVM:当数据是线性可分时,能够运用线性SVM来找到最优超平面。线性SVM经过最大化两类数据点之间的距离来完成这一点。
3. 非线性SVM:当数据不是线性可分时,能够运用非线性SVM来找到最优超平面。非线性SVM经过运用核函数将数据映射到高维空间,然后使得数据变得线性可分。
4. 核函数:核函数是SVM中用于将数据映射到高维空间的函数。常用的核函数包含线性核、多项式核、径向基函数(RBF)核等。
5. 软距离:在实践运用中,数据往往不是彻底线性可分的。为了处理这个问题,SVM引入了“软距离”的概念。软距离答应一些数据点坐落超平面的过错侧,但会对这些数据点进行赏罚。
6. 参数调整:SVM的功能壬能精确地猜测接连的输出值。
9. SVM的优缺陷:SVM的长处包含强壮的泛化才能、对异常值不灵敏等。SVM的缺陷包含练习时刻较长、对参数挑选灵敏等。
10. 运用范畴:SVM在许多范畴都有运用,如文本分类、图像辨认、生物信息学等。
支撑向量机(Support Vector Machine,简称SVM)是一种强壮的监督学习算法,广泛运用于分类和回归问题。本文将深化解析SVM的原理、运用场景以及优缺陷,协助读者更好地了解这一机器学习算法。
支撑向量机的基本思想是经过结构一个超平面(Hyperplane)来将不同类其他数据点分隔,使得类之间的距离最大化。换句话说,SVM企图找到一个最优的决议计划鸿沟,使得不同类其他点在该鸿沟的两边有最大的距离,然后进步分类的精确性和泛化才能。
SVM的数学原理依据优化问题,经过最大化分类距离来完成分类。以下将经过数学推导具体介绍其基本原理。

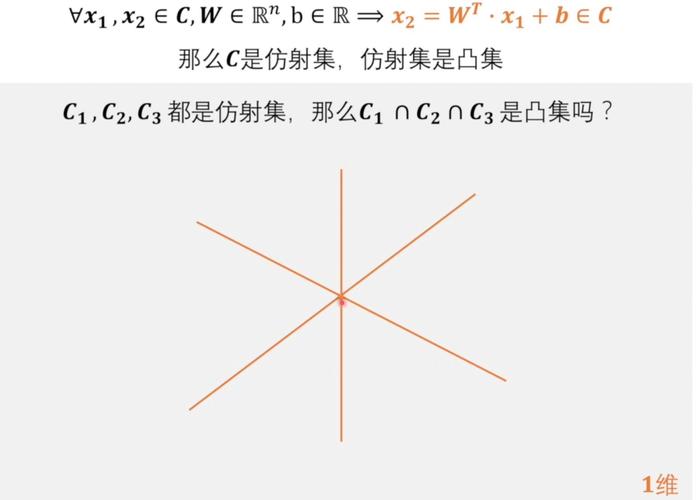
为了找到最优的超平面,咱们需求处理一个最优化问题。具体来说,咱们需求最大化以下方针函数:
最大化距离:maximize (1/2) ||w||^2,其间 ||w|| 表明向量 w 的欧几里得范数。
因为方针函数中存在约束条件,咱们需求运用拉格朗日对偶问题来求解。拉格朗日对偶问题将原始问题转化为一个无约束的优化问题,然后更简单求解。
当数据不行线性切割时,SVM经过核技巧将数据映射到更高维的空间,使得本来不行分的状况变得可分。常用的核函数包含线性核、多项式核、高斯核(RBF)和Sigmoid核等。

SVM具有杰出的泛化才能,在许多实践问题中体现出色。以下罗列一些SVM的运用场景:
垃圾邮件过滤、情感剖析等。

手写数字辨认、面部辨认等。
癌症确诊、蛋白质结构猜测等。
信誉评分、股票市场猜测等。
疾病分类等。
4.1 长处
1. 合适高维数据:在高维数据中仍体现杰出。
2. 非线性处理才能强:经过核技巧处理非线性问题。
3. 泛化才能强:经过最大化距离进步模型的鲁棒性。
4.2 缺陷
1. 核算复杂度高:在处理大规划数据集时,SVM的核算复杂度较高。
2. 对参数灵敏:SVM的参数较多,需求依据具体问题进行调整。
3. 不适用于大规划数据集:当数据集规划较大时,SVM的练习和猜测速度较慢。
支撑向量机(SVM)是一种强壮的监督学习算法,在许多实践问题中体现出色。本文从基本概念、数学原理、运用场景、优缺陷等方面对SVM进行了深化解析,期望对读者有所协助。