机器学习 回归算法,二、回归算法的基本概念

机器学习中的回归算法是一种用于猜测接连数值的猜测办法。它经过树立输入特征和输出方针之间的数学联系，来猜测不知道数据点的数值。回归算法广泛使用于各种范畴，如金融猜测、房价猜测、销量猜测等。

回归算法的首要方针是找到一个函数，该函数能够最小化猜测值与实践值之间的差异。这个函数一般是一个线性函数，但在某些情况下，或许需求运用非线性函数来更好地拟合数据。

以下是几种常见的回归算法：

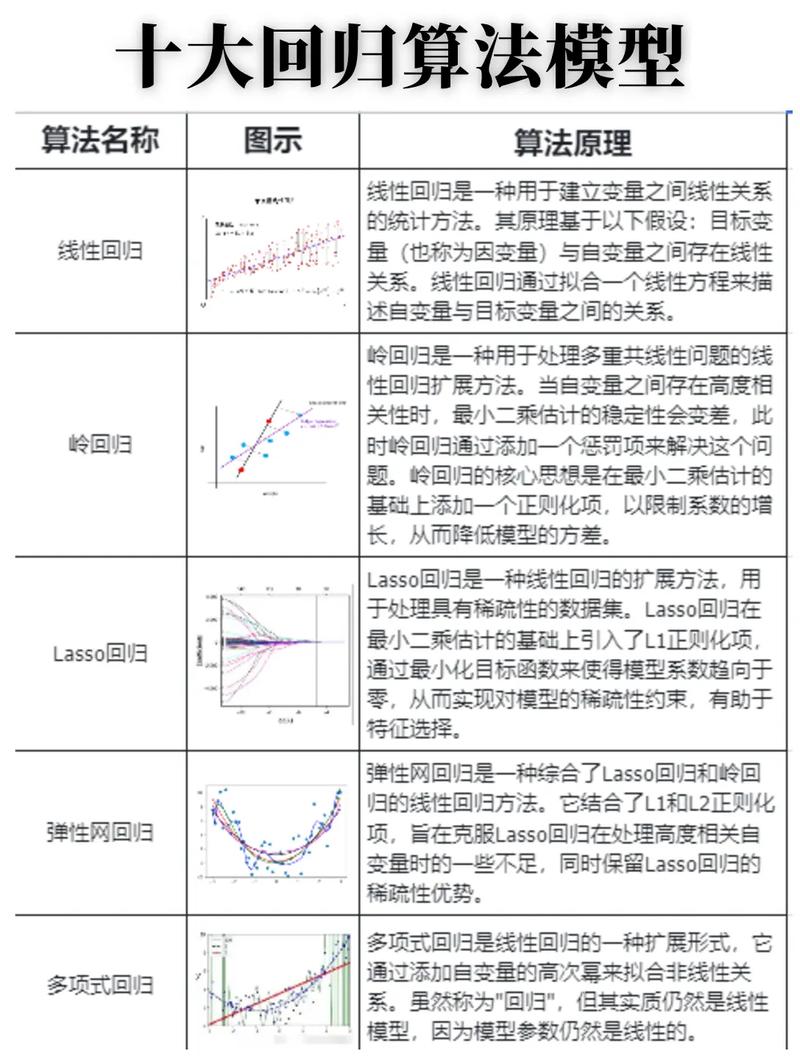
1. 线性回归（Linear Regression）：线性回归是最基本的回归算法，它假定输入特征和输出方针之间存在线性联系。线性回归的方针是找到一个线性方程，使得猜测值与实践值之间的差异最小。

2. 决策树回归（Decision Tree Regression）：决策树回归是一种依据决策树的回归算法。它经过递归地切割数据集，将数据集划分为更小的子集，并在每个子集上树立回归模型。决策树回归能够处理非线性联系，而且具有很好的解说性。

3. 随机森林回归（Random Forest Regression）：随机森林回归是一种依据决策树的集成学习算法。它经过构建多个决策树，并将它们的猜测成果进行均匀，来进步猜测的准确性。随机森林回归能够处理非线性联系，而且对噪声数据具有较好的鲁棒性。

4. 支撑向量回归（Support Vector Regression）：支撑向量回归是一种依据支撑向量机的回归算法。它经过找到一个超平面，使得猜测值与实践值之间的差异最小。支撑向量回归能够处理非线性联系，而且具有很好的泛化才能。

5. 神经网络回归（Neural Network Regression）：神经网络回归是一种依据神经网络的回归算法。它经过构建一个多层神经网络，将输入特征映射到输出方针。神经网络回归能够处理杂乱的非线性联系，而且具有很好的泛化才能。

这些回归算法各有优缺陷，挑选适宜的回归算法需求依据具体问题和数据的特点来决议。在实践使用中，一般需求经过穿插验证等办法来评价不同回归算法的功能，并挑选功能最好的算法进行猜测。

深化解析机器学习中的回归算法

在机器学习范畴，回归算法是一种重要的猜测建模技能。它经过树立因变量与自变量之间的数学联系，协助咱们猜测和剖析数据。本文将深化解析机器学习中的回归算法，包含其基本概念、常用算法、优缺陷以及实践使用。

二、回归算法的基本概念

回归算法旨在经过剖析历史数据，树立因变量与自变量之间的数学模型，然后对不知道数据进行猜测。在回归问题中，因变量一般是接连的，而自变量可所以接连的或离散的。

三、常用回归算法

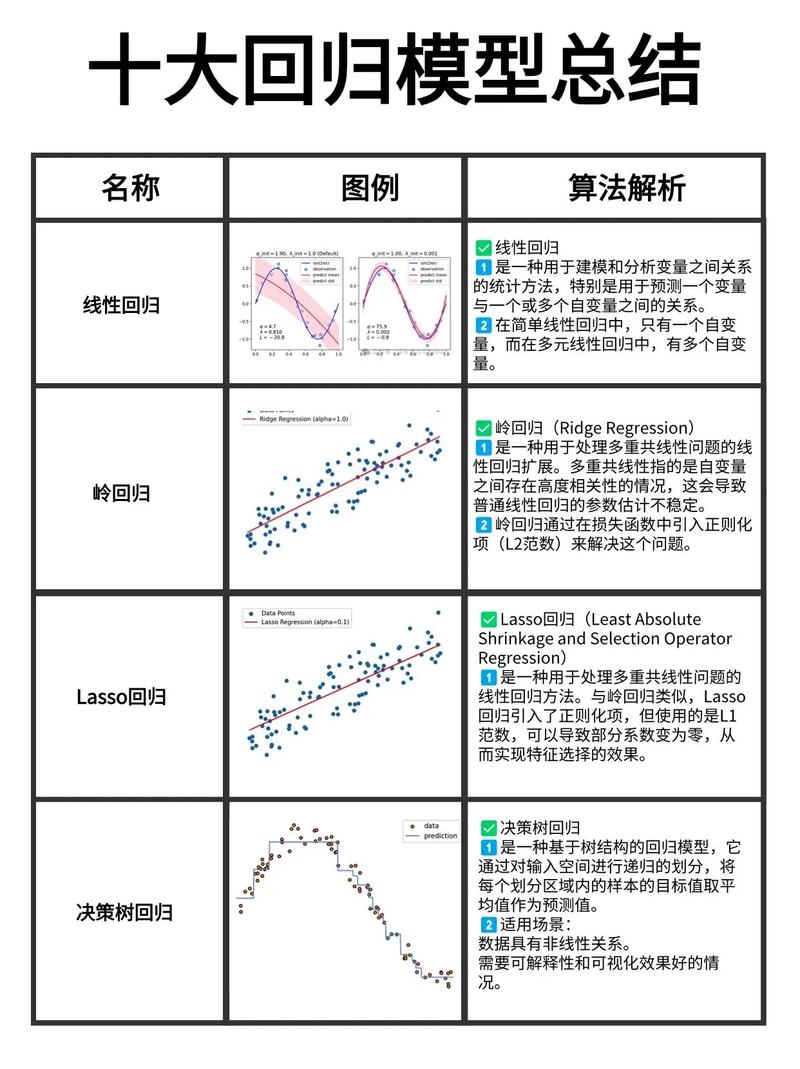
1. 线性回归

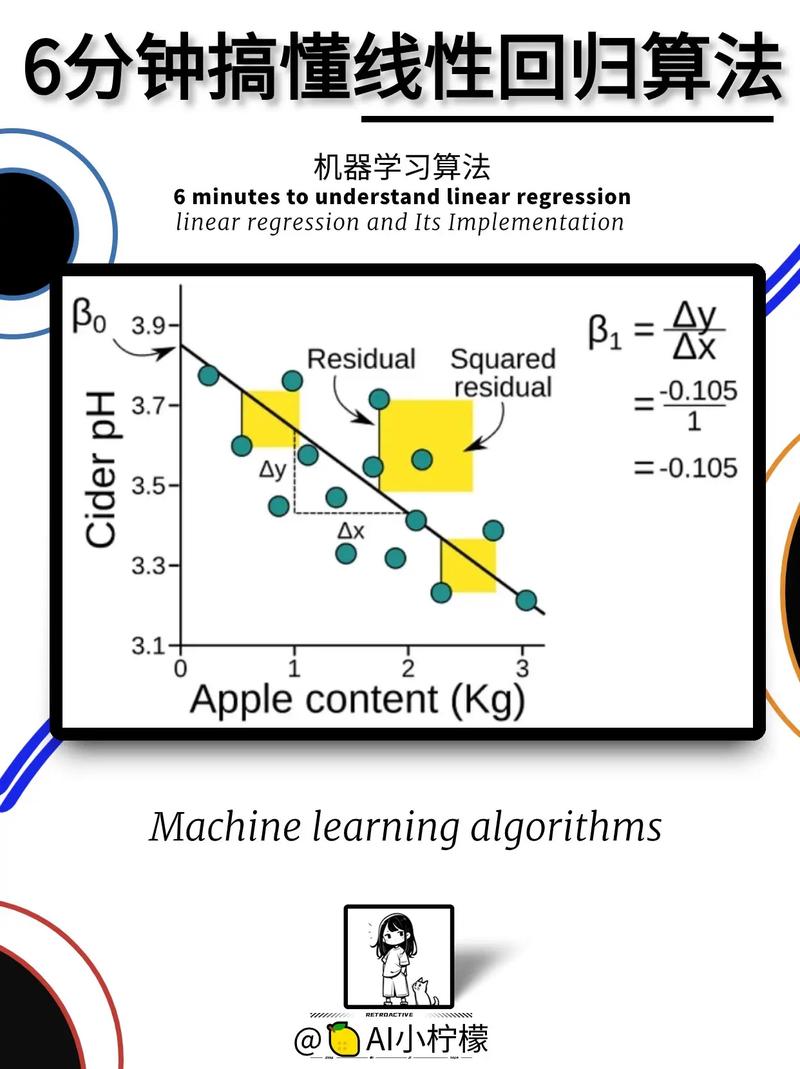
线性回归是最基本的回归算法，它假定因变量与自变量之间存在线性联系。线性回归模型能够表明为：y = β0 β1x1 β2x2 ... βnxn ε，其间y为因变量，x1, x2, ..., xn为自变量，β0, β1, ..., βn为模型参数，ε为差错项。

2. 逻辑回归

逻辑回归是一种特别的线性回归，用于处理二分类问题。它经过Sigmoid函数将线性回归的输出映射到(0, 1)区间，然后得到一个概率值，表明样本归于某一类的或许性。

3. 多元线性回归

多元线性回归是线性回归的扩展，它考虑多个自变量对因变量的影响。多元线性回归模型能够表明为：y = β0 β1x1 β2x2 ... βnxn ε，其间y为因变量，x1, x2, ..., xn为自变量，β0, β1, ..., βn为模型参数，ε为差错项。

4. 逐渐回归

逐渐回归是一种依据模型挑选原则的回归算法，它经过逐渐挑选最优的自变量，树立回归模型。逐渐回归能够有效地处理高维数据，进步模型的猜测精度。

四、回归算法的优缺陷

1. 长处

（1）易于了解和完成；

（2）适用于多种数据类型；

（3）能够处理高维数据；

（4）模型参数易于解说。

2. 缺陷

（1）对异常值灵敏；

（2）假定因变量与自变量之间存在线性联系，或许不适用于非线性问题；

（3）模型参数较多，或许存在过拟合现象。

五、回归算法的实践使用

回归算法在各个范畴都有广泛的使用，以下罗列一些常见的使用场景：

（1）金融范畴：股票价格猜测、信誉评分、危险评价等；

（2）医疗范畴：疾病猜测、药物效果评价、患者预后等；

（3）工业范畴：产品质量猜测、设备毛病猜测、生产过程优化等。

回归算法是机器学习范畴的重要东西，它能够协助咱们树立因变量与自变量之间的数学模型，然后对不知道数据进行猜测。本文对回归算法的基本概念、常用算法、优缺陷以及实践使用进行了深化解析，期望对读者有所协助。