机器学习是一个触及多个范畴的学科,其间包含数学、统计学、核算机科学等。在机器学习中,数学扮演着至关重要的人物,由于它供给了了解、规划和完成各种机器学习算法的理论根底。
1. 线性代数:线性代数是机器学习的根底,它包含向量、矩阵、线性方程组、特征值和特征向量等概念。线性代数在数据表明、特征提取、模型练习和猜测等方面都有广泛运用。
2. 概率论和统计学:概率论和统计学是了解数据、评价模型功能和做出决议计划的根底。在机器学习中,咱们常常运用概率散布、随机变量、期望值、方差、协方差、概率密度函数等概念来描绘数据散布和模型的不确定性。
3. 微积分:微积分在机器学习中的运用包含优化问题、梯度下降、丢失函数的求导等。经过微积分,咱们可以找到函数的最小值或最大值,这关于练习机器学习模型非常重要。
4. 信息论:信息论是研讨信息、不确定性、熵和互信息等概念的学科。在机器学习中,信息论用于衡量数据的不确定性、模型复杂性和信息增益等。
5. 最优化理论:最优化理论是研讨怎么找到函数的最优解的学科。在机器学习中,咱们常常运用最优化算法来练习模型,例如梯度下降、牛顿法、共轭梯度法等。
6. 图论:图论是研讨图(由节点和边组成)的数学分支。在机器学习中,图论用于表明数据之间的联系、构建网络结构、进行图神经网络等。
7. 复杂性理论:复杂性理论是研讨问题处理的时刻和空间复杂性的学科。在机器学习中,复杂性理论用于评价算法的功率,挑选适宜的模型和算法。
8. 数值剖析:数值剖析是研讨数值核算办法的理论根底。在机器学习中,数值剖析用于处理线性方程组、非线性方程组、优化问题等。
这些数学概念和东西为机器学习供给了强壮的理论根底,使得咱们可以更好地了解、规划和完成各种机器学习算法。机器学习是一个不断发展的范畴,跟着新算法和新技术的呈现,对数学的要求也在不断提高。因而,关于从事机器学习的研讨人员来说,不断学习和把握新的数学知识是非常重要的。
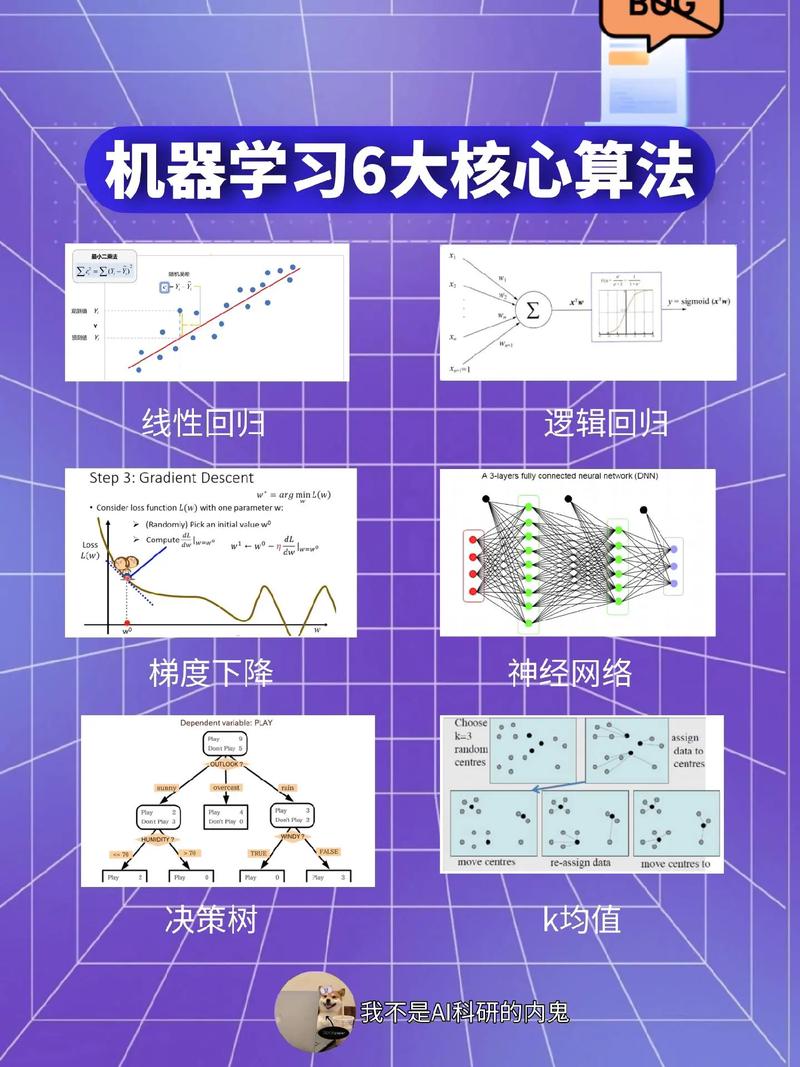
机器学习作为人工智能范畴的一个重要分支,其中心在于经过算法从数据中学习并做出猜测或决议计划。而这一切的完成都离不开数学的支撑。本文将扼要介绍机器学习中的数学根底,协助读者了解数学在机器学习中的重要性。
概率论是机器学习的根底,它供给了处理不确定性和随机性的数学东西。在机器学习中,概率论用于描绘数据散布、模型参数的估量以及模型猜测的不确定性。数理统计则是概率论在数据剖析中的运用,包含假设检验、参数估量和置信区间等。

线性代数是机器学习中不可或缺的数学东西,它触及向量、矩阵、行列式等概念。在机器学习中,线性代数用于处理数据表明、特征提取、降维和优化等问题。例如,主成分剖析(PCA)便是一种根据线性代数的降维办法。
数值核算是机器学习中的另一个重要数学分支,它触及数值剖析、算法规划和数值稳定性等问题。在机器学习中,数值核算用于求解优化问题、核算梯度、更新模型参数等。常见的数值核算办法包含牛顿法、梯度下降法等。

信息论是研讨信息传输、存储和处理的理论。在机器学习中,信息论用于衡量数据之间的相似性、信息熵、穿插熵等。信息论在特征挑选、模型挑选和模型评价等方面发挥着重要效果。
最优化理论是机器学习中处理优化问题的数学东西。在机器学习中,最优化理论用于求解模型参数、特征挑选、模型挑选等问题。常见的最优化算法包含梯度下降法、牛顿法、共轭梯度法等。
以下罗列几个机器学习中的数学运用实例,以协助读者更好地了解数学在机器学习中的效果。
线性回归:线性回归是一种常用的猜测办法,它经过最小化猜测值与实践值之间的差错来拟合数据。线性回归的数学根底是线性代数和最优化理论。
支撑向量机(SVM):SVM是一种分类算法,它经过寻觅最优的超平面来将数据分为不同的类别。SVM的数学根底是线性代数和最优化理论。
深度学习:深度学习是一种根据人工神经网络的机器学习办法,它经过多层神经网络来提取数据特征。深度学习的数学根底包含线性代数、概率论、最优化理论和数值核算。
机器学习中的数学根底是构建高效、精确的机器学习模型的要害。把握这些数学知识,有助于咱们更好地了解和运用机器学习算法。本文扼要介绍了机器学习中的数学根底,期望对读者有所协助。
下一篇: AI归纳运用课程,敞开智能年代的学习之旅